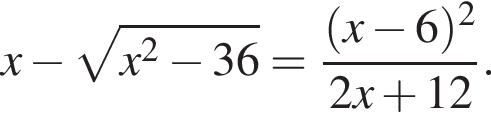Образующая конуса равна 26 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
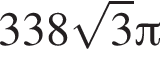

Образующая конуса равна 26 и наклонена к плоскости основания под углом 60°. Найдите площадь боковой поверхности конуса.
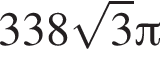

Прямые a и b, пересекаясь, образуют четыре угла. Известно, что сумма трех углов равна 210°. Найдите градусную меру меньшего угла.
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,9 | |
| b | 108 | 7,6 |
Укажите номер выражения, являющегося одночленом восьмой степени:
а) 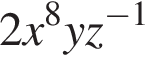 | б) 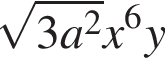 | в) | г) 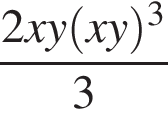 | д) |
Функция y = f(x) задана на множестве действительных чисел и является убывающей на области определения. Среди ее значений 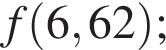



![]() укажите наибольшее.
укажите наибольшее.
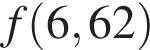
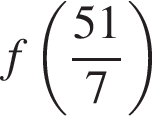
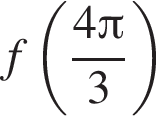

Четырехугольник MNPK, в котором ∠N = 128°, вписан в окружность. Найдите градусную меру угла K.
Уравнение 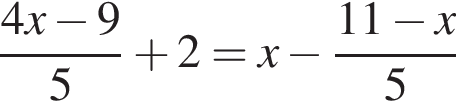 равносильно уравнению:
равносильно уравнению:



Пусть x1 и x2 — корни уравнения 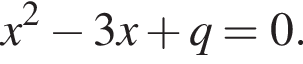 Найдите число q, при котором выполняется равенство
Найдите число q, при котором выполняется равенство 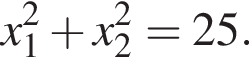
Диаметр окружности пересекает хорду под углом 60° и точкой пересечения делит ее на отрезки длиной 2 и 12. Найдите квадрат радиуса окружности.
Найдите сумму всех целых решений неравенства 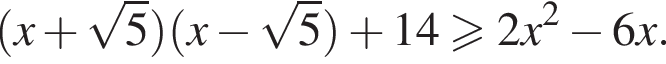
Диагонали трапеции равны 15 и 20. Найдите площадь трапеции, если ее средняя линия равна 12,5.
Точки А(1;2), B(5;6) и C(8;6) — вершины трапеции ABCD (AD||BC). Найдите сумму координат точки D, если 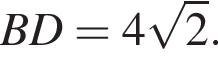
Известно, что при a, равном −2 и 4, значение выражения 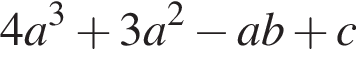 равно нулю. Найдите значение выражения b + с.
равно нулю. Найдите значение выражения b + с.
Выберите три верных утверждения:
1) если 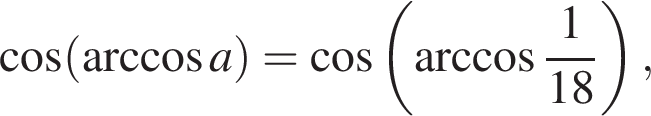 то
то 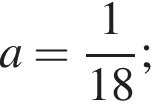
2) если 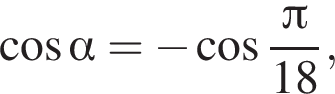 то
то 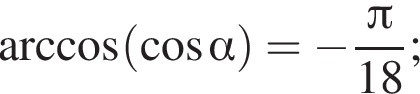
3) если 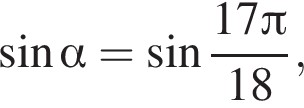 то
то 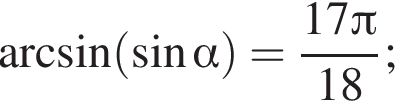
4) если 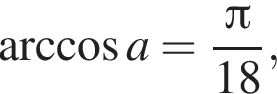 то
то 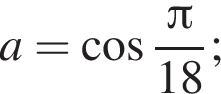
5) если 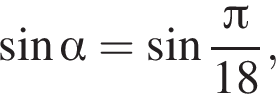 то
то 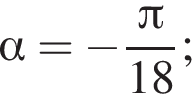
6) если 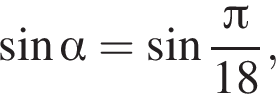 то
то 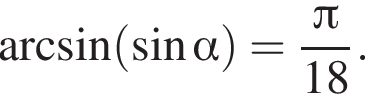
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Дана геометрическая прогрессия (bn), в которой b5 = −12, b6 = 36. Для начала каждого из предложений А−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Знаменатель этой прогрессии равен ...
Б) Четвертый член этой прогрессии равен ...
В) Первый член этой прогрессии равен ...
1) −4
2) ![]()
3) ![]()
4) −3
5) 4
6) ![]()
Oтвет запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
На диаграмме показано количество всех покупателей интернет-магазина (П) и количество покупателей, совершивших более одной покупки (ПБ), за период шесть месяцев (с июля по декабрь). Установите соответствие между вопросами А−В и ответами 1−6.
A) В каком месяце количество всех покупателей было наибольшим?
Б) В каком месяце количество покупателей, совершивших более одной покупки, было 160?
В) В каком месяце количество покупателей, совершивших более одной покупки, составило 20% от количества всех покупателей в этом месяце?
1) Июль
2) Август
3) Сентябрь
4) Октябрь
5) Ноябрь
6) Декабрь
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например, А1Б1В4.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите сумму всех натуральных чисел a, для которых выполняется равенство 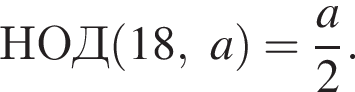
Найдите сумму целых решений неравенства 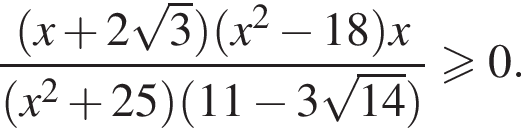
Найдите значение выражения 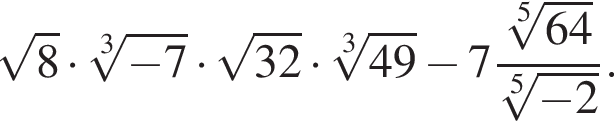
Найдите сумму всех целых решений неравенства 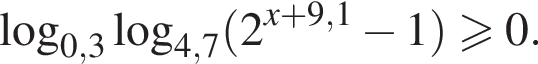
О натуральных числах а и b известно, что 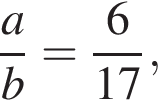 НОД(a; b) = 4. Найдите НОК(a + b; 10).
НОД(a; b) = 4. Найдите НОК(a + b; 10).
Найдите значение выражения 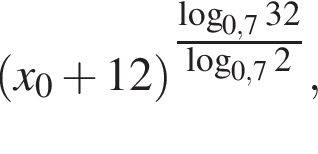 где x0 — корень уравнения
где x0 — корень уравнения 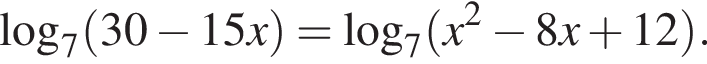
На рисунке изображен график функции 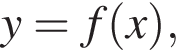 заданной на промежутке
заданной на промежутке 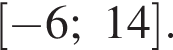 Найдите произведение значений аргумента, при которых
Найдите произведение значений аргумента, при которых 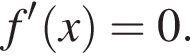 (Черными точками отмечены узлы сетки, через которые проходит график функции
(Черными точками отмечены узлы сетки, через которые проходит график функции 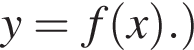
Найдите значение выражение 
Найдите произведение наибольшего отрицательного и наименьшего положительного целых решений неравенства 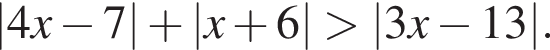
В прямоугольный треугольник AOB, катеты которого OA и OB (OA > OB) лежат соответственно на координатных осях Ox и Oy, вписана окружность радиуса 10. Найдите сумму координат точки касания окружности и гипотенузы AB, если треугольник AOB лежит в первой четверти координатной плоскости и его площадь равна 600.
Прямоугольный треугольник с катетами, равными 6 и ![]() вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения
вращается вокруг оси, содержащей его гипотенузу. Найдите значение выражения ![]() где V — объём фигуры вращения.
где V — объём фигуры вращения.
Найдите произведение наибольшего целого решения на количество всех натуральных решений неравенства 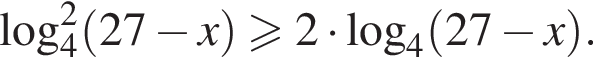
Найдите произведение корней уравнения